Problema del prodotto palindromico perplesso

Question

Ho imparato Ruby, quindi ho pensato di provare la mia mano ad alcuni dei puzzle di Eulero del progetto. Imbarazzante, ho fatto solo per problema 4 ...

Problema 4 va come segue:

Un numero palindromo legge gli stessi in entrambe le direzioni. Il più grande palindromo fatto dal prodotto di due 2 cifre numeri è 9009 = 91 × 99.

Trova il più grande palindromo fatto da il prodotto di due numeri a 3 cifre.

Così ho pensato che avrei ciclo giù 999-100 in un nidificato ciclo for e fare un test per il palindromo e poi uscire dai loop quando ho trovato il primo (che dovrebbe essere il più grande) :

final=nil 
range = 100...1000 
for a in range.to_a.reverse do 
    for b in range.to_a.reverse do 
    c=a*b 
    final=c if c.to_s == c.to_s.reverse 
    break if !final.nil? 
    end 
    break if !final.nil? 
end 
puts final 

questo fa produrre un palindromo 580085, ma a quanto pare questo non è il più alto prodotto di due numeri a tre cifre all'interno della gamma. Stranamente, lo stesso codice riesce a restituire 9009, come nell'esempio, se cambio l'intervallo su 10 ... 100.

• Qualcuno può dirmi dove sto andando sbagliato?
• Inoltre, c'è un modo più bello di uscire dal ciclo interno ?

Grazie

Answer 1

Si stanno testando 999 * (999 ... 100), quindi 998 * (999 ... 100)

Quindi sarete testando 999 * 500 prima di testare 997 * 996.

Quindi, come lo troviamo giusto numero?

Innanzitutto, la moltiplicazione è riflettente, a * b == b * a, quindi b non deve passare da 999 ... 0 ogni volta, solo a ... 0.

Quando si trova un Palindrone, aggiungere i due fattori insieme e salvare la somma (salvare i due fattori anche)

All'interno del ciclo, se (a + b) è sempre inferiore alla somma salvato, abbandonare la anello interno e passare al successivo a. Quando scende sotto la somma/2, nessun valore futuro che potresti trovare sarebbe più alto di quello che hai già trovato, quindi hai finito.

Answer 2

L'errore si è scontato che se si trova Palindrom con maggior valore a darà il più grande prodotto che non è vero. La soluzione è mantenere il valore max_product e aggiornarlo contro la soluzione trovata.

Answer 3

Posso rispondere alla prima domanda: è necessario trovare il prodotto più alto, non il prodotto che contiene il fattore più alto. In altre parole, a * b potrebbe essere maggiore di c * d anche se c > a > b.

Answer 4

Il problema è che potresti trovare un palindromo per un a di 999 e uno b di 200, ma si interrompe troppo presto, quindi non si vede mai che ce ne sia uno per 998 * 997 (solo numeri di esempio).

È necessario cercare tutti i palindromi o una volta trovato il primo, impostare b come limite minimo e continuare a guardare attraverso il ciclo a.

Answer 5

Stai rompendo il primo palindromo in cui sei arrivato, non necessariamente il più grande.

Supponiamo di avere A, B, C, D, E. Si prova E * A prima di testare D * C.

Answer 6

Per quanto riguarda la seconda domanda, il mio consiglio è di affrontare il problema in modo più funzionale, che procedurale. Così, invece di loop, si può tentare di "descrivere" il problema funzionale, e lasciare Rubino fa il lavoro:

• Da tutte le coppie di numeri a 3 cifre,
  • solo quelli il cui prodotto select è un palindromo,
    • e trovare quello con il più grande prodotto

Anche se questo approccio potrebbe non produrre la soluzione più efficiente, potrebbe insegnarti una coppia di espressioni Ruby.

Answer 7

un'implementazione:

max = 100.upto(999).inject([-1,0,0]) do |m, a| 
    a.upto(999) do |b| 
    prod = a * b 
    m = [prod, a, b] if prod.to_s == prod.to_s.reverse and prod > m[0] 
    end 
    m 
end 
puts "%d = %d * %d" % max 

stampe 906609 = 913 * 993

Answer 8

La cosa principale è quello di passare attraverso tutti i possibili valori. Non cercare di interrompere quando trovi la prima risposta, inizia semplicemente con una migliore risposta pari a zero, quindi prova tutte le combinazioni e mantieni l'aggiornamento migliore. La cosa secondaria è cercare di ridurre il set di "tutte le combinazioni".

Una cosa che si può fare è limitare il ciclo interno a valori inferiori o uguali a a (dal b == b a). Ciò mette il valore più grande della tua equazione sempre in a e riduce sostanzialmente il numero di valori che devi testare.

for a in range.to_a.reverse do 
    for b in (100..a).to_a.reverse do 

La prossima cosa che puoi fare è uscire dal ciclo interno ogni volta che il prodotto è inferiore al miglior valore corrente.

c = a*b 
next if c < best 

Avanti, se avete intenzione di passare attraverso di loro tutti in ogni caso non c'è alcun beneficio per passare attraverso di loro in senso inverso. Iniziando in cima alla gamma ci vuole un po 'prima di trovare un numero palindromico e di conseguenza ci vuole un po' per ridurre il set di ricerca. Se inizi in basso, inizi ad aumentare rapidamente il limite inferiore.

for a in range.to_a do 
    for b in (100..a).to_a do 

I miei test mostrano comunque che si provano alcune coppie 405K. Che ne dici di pensare al problema in un modo diverso. Qual è il più grande prodotto possibile di due numeri a 3 cifre?999 * 999 = 998001 e il più piccolo è 100 * 100 = 10000. Che ne dici se pensiamo di aver infranto la prima risposta ma di applicarla a un intervallo diverso, da 998001 a 10000 (o 999 * 999 a 100 * 100).

for c in (10000...998001).to_a.reverse do 

si arriva a un palindromo dopo soli 202 test ... il problema è che non è un prodotto di due numeri a 3 cifre. Quindi ora dobbiamo verificare se il palindrome che abbiamo trovato è un prodotto di 2 numeri a 3 cifre. Non appena troviamo un valore nell'intervallo che è un palindromo e un prodotto di due numeri a 3 cifre, abbiamo finito. I miei test mostrano che troviamo il palindromo più alto che soddisfa il requisito dopo meno di 93K test. Ma dal momento che abbiamo il sovraccarico di controllare che tutti i palindromi a quel punto fossero prodotti da due numeri a 3 cifre, potrebbe non essere più efficiente della soluzione precedente.

Quindi, torniamo al miglioramento originale.

for a in range.to_a.reverse do 
    for b in (100..a).to_a.reverse do 

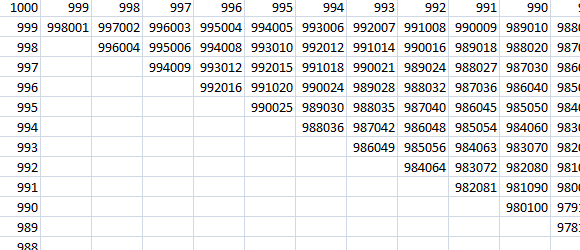
Stiamo looping righe poi colonne e cercando di essere efficiente rilevando un punto in cui possiamo andare alla riga successiva in quanto qualsiasi trys aggiuntivi sulla riga corrente non potevano essere migliore di nostro attuale migliore. Cosa succede se, invece di scendere le file, attraversiamo le diagonali?

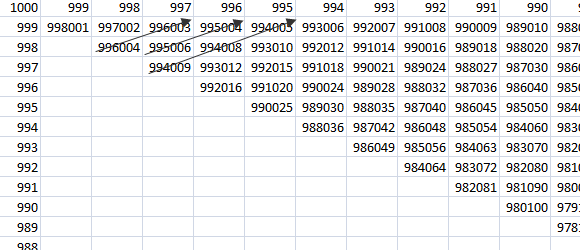
Dal momento che i prodotti diventano più piccoli diagonale dalla diagonale si può fermare, non appena si trova un numero palindome. Questa è una soluzione davvero efficiente ma con un'implementazione più complessa. Si scopre che questo metodo trova il palindromo più alto dopo poco più di 2200 tris.

Answer 9

Considera le cifre di P - lasciale essere x, yez. P deve essere lungo almeno 6 cifre dal palindrome 111111 = 143 × 777 - il prodotto di due numeri interi a 3 cifre. Dal momento che P è palindromo:

P=100000x + 10000y + 1000z + 100z + 10y + x 
P=100001x + 10010y + 1100z 
P=11(9091x + 910y + 100z) 

Dal 11 è primo, almeno uno degli interi a o b deve avere un fattore di 11. Quindi, se un non è divisibile per 11 allora sappiamo b deve essere. Usando queste informazioni possiamo determinare quali valori di b controlliamo in base a a.

Answer 10

C# Implementazione:

using System; 

namespace HighestPalindrome 
{ 
    class Program 
    { 
     static void Main(string[] args) 
     { 
      int i, j; 
      int m = 1; 
      bool flag = false; 

      while (true) 
      { 
       if (flag) j = m + 1; 
       else j = m; 

       for (i = m; i > 0; i--) 
       { 
        Console.WriteLine("{0} * {1} = {2}", 1000 - i, 1000 - j, (1000 - i) * (1000 - j)); 
        j++; 

        //--- Palindrome Check ------------------------------ 

        int number, temp, remainder, sum = 0; 
        number = temp = (1000 - i) * (1000 - j); 

        while (number > 0) 
        { 
         remainder = number % 10; 
         number /= 10; 
         sum = sum * 10 + remainder; 
        } 

        if (sum == temp) 
        { 
         Console.WriteLine("Highest Palindrome Number is - {0} * {1} = {2}", 1000 - i, 1000 - j, temp); 
         Console.ReadKey(); 
         return; 
        } 

        //--------------------------------------------------- 
       } 

       if (flag) 
        m++; 
       flag = !flag; 
      } 

     } 
    } 
} 

Answer 11

ar=[] 
limit = 100..999 
for a in limit.to_a.reverse do 
    for b in (100..a).to_a.reverse do 
    c=a*b 
    if c.to_s == c.to_s.reverse 
     palndrm=c 
     ar << palndrm 
    end 
    end 
end 
print ar 
print"\n" 
puts ar.max 
puts ar.min 

Answer 12

Ecco cosa mi è venuta in Ruby:

def largest_palindrome_product(digits) 
    largest, upper, lower = 0, 10**digits - 1, 10**(digits - 1) 

    for i in upper.downto(lower) do 
    for j in i.downto(lower) do 
     product = i * j 
     largest = product if product > largest && palindrome?(product) 
    end 
    end 
    largest 
end 

Ed ecco la funzione per controllare se il numero è un palindromo:

def palindrome?(input) 
    chars = input.to_s.chars 
    for i in 0..(chars.size - 1) do 
    return false if chars[i] != chars[chars.size - i - 1] 
    end 
    true 
end 

Immagino che ci sia probabilmente più efficacia soluzione nt là fuori, però.

Answer 13

Per questo problema, poiché stiamo cercando il palindrom più alto, ho pensato che sarebbe iniziato con un 9. Finendo così con un 9 (palindrom).

se si presta attenzione, per ottenere un numero di finitura del 9, si può ottenere solo con finitura numeri 9 e 1, 3 e 3, 7 e 7.

Poi è inutile controllare l'altra valori (ad esempio 999 * 998 in quanto non termina con un 9).

A partire dal 999 e 991, è quindi possibile sottrarre 10 a 991, provando 999 e 981 ecc ... Si fa lo stesso con 993 e 993 ...993 * 983 stesso con 997 * 997 quindi 997 * 987, ecc. Non è necessario andare oltre 900 o 10^4 - 10^3 poiché si può essere sicuri che il massimo sarà prima.

int PB4_firstTry(int size) 
{ 
    int nb1 = (int)pow(10.0,size+1.0) - 1, nb2 = (int)pow(10.0,size+1.0) - 1; 
    int pal91 = getFirstPalindrome(size,9,1); 
    int pal33 = getFirstPalindrome(size,3,3); 
    int pal77 = getFirstPalindrome(size,7,7); 

    int bigger1 = (pal91 > pal33) ? pal91 : pal33; 
    return (bigger1 > pal77) ? bigger1 : pal77; 
} 

int getFirstPalindrome(int size,int ending1,int ending2) 
{ 
    int st1 = (int)pow(10.0,size+1.0) - 10 + ending1; 
    int comp = st1 - pow(10.0,size); 
    int st2 = (int)pow(10.0,size+1.0) - 10 + ending2; 
    int answer = -1; 
    while (st1 > comp) 
    { 
     for (int i = st2; i > comp && st1*i > answer; i-=10) 
     { 
      if (PB4_isPalindrome(st1*i)) 
       answer = st1*i; 
     } 
     st1 -= 10; 
    } 
    return answer; 
} 

bool PB4_isPalindrome(int number) 
{ 
    std::string str = intToString(number); 
    for (int i = 0; i < (int)(str.length()/2); i++) 
    { 
     if (str[i] != str[str.length() - 1 - i]) 
      return false; 
    } 
    return true; 
} 

std::string intToString(int number) 
{ 
    std::ostringstream convert; 
    convert << number; 
    return convert.str(); 
} 

Naturalmente, questo funziona per 4 fattori cifre dimensioni ecc