Uno degli approcci seguenti utilizza la matematica corretta per la rotazione di un punto? Se sì, quale è corretto?Trigonometria corretta per la rotazione di un punto intorno all'origine
POINT rotate_point(float cx,float cy,float angle,POINT p)
{
float s = sin(angle);
float c = cos(angle);
// translate point back to origin:
p.x -= cx;
p.y -= cy;
// Which One Is Correct:
// This?
float xnew = p.x * c - p.y * s;
float ynew = p.x * s + p.y * c;
// Or This?
float xnew = p.x * c + p.y * s;
float ynew = -p.x * s + p.y * c;
// translate point back:
p.x = xnew + cx;
p.y = ynew + cy;
}

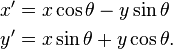
I don' t abbastanza comprensibile. Cosa sono cx e cy? Inoltre, hai dichiarato la tua funzione di tipo POINT, ma non restituisce un PUNTO, o anzi nulla. –
@Brian Hooper: +1 per indicare i vantaggi di nomi di variabili significative;) – Cogwheel