Come determinare per quale valore verrà attivato il neurone artificiale?

Question

Sto provando a determinare per il neurone articolare mostrato sotto i valori (0 o 1) per gli ingressi i1, i2 e i3 per i quali si spara (i0 è l'input per il peso bias e sarà sempre -1).

I pesi sono

W0 = 1,5

W1 = -1

W2 = 1, e W3 = 2.

assumere la funzione di attivazione illustrato nella figura qui sotto.

Si prega di chiarire la vostra risposta come ho fatto alcuni esempi ed ancora non sono in grado di comprendere appieno la teoria :(

Molte grazie,

Mary J.

PS. immagine di seguito:

Answer 1

Hai sostanzialmente la seguente equazione per l'uscita neurone, dove i1, i2 e i3 possibile ogni avere il valore 0 o 1:

2*i3 + i2 - i1 - 1.5 >= 0 

In primo luogo, diamo un'occhiata al valore con valore positivo più elevato. Se i3 è 0, il massimo che puoi ottenere per il lato sinistro è -0.5, quindi i3 deve essere 1 per ottenere un output diverso da zero. L'equazione diventa allora:

i2 - i1 + 0.5 >= 0 

Ora guardate al valore negativo ponderato. Se i1 è 0, l'uscita sarà sempre maggiore di zero indipendentemente da cosa sia i2. Se i1 è 1, i2 deve essere 1 anche perché ci sia un'uscita diversa da zero.

Si hanno quindi queste combinazioni che creano un'uscita diverso da zero:

i1 i2 i3 

0  0  1 
0  1  1 
1  1  1 

Answer 2

sembra di essere come se fosse solo am di sommare in * Wn e determinare quali combinazioni di i1,2,3 danno un risultato positivo. Ci sono solo 8 permutazioni, quindi percorrilo a mano.

Answer 3

ho conoscenza superficiale di intelligenza artificiale, ma per quanto ne so:

La somma degli input (Sigma i_n * W_n) deve essere superiore alla soglia di sparo. la seconda immagine ti dice la soglia di fuoco, la prima immagine ti dice gli input e i loro pesi.

Basta capire quale somme (non dimenticare il bias) comporterà soglia/intensità desiderata

Answer 4

Per risolvere questo problema in modo più generale, primo sguardo a quali sono le variabili e quali sono i parametri fissi.

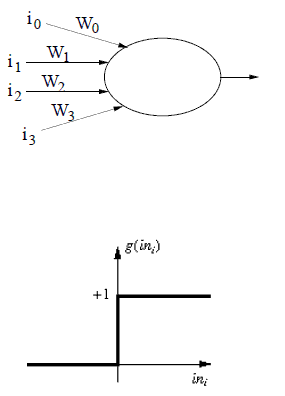
In sostanza si è data l'ingresso pesi vettore w= [1.5, -1, 1, 2] e la funzione di trasferimentog(x) = (sign(x)+1)/2, e si desidera trovare il ingresso vettore in in modo che: g(w*in') = +1 (come prodotto di un vettore riga e colonna), quindi:

g(sum_over_i(w_i*in_i)) = 1    # product of vectors 
g(w0*in0 + w1*in1 + w2*in2 + w3*in3) = 1  # roll out the sum 
g(-1.5 - in1 + in2 + 2*in3) = 1    # replace the values of w and in 
0.5*(sign(-1.5 - in1 + in2 + 2*in3)+1) = 1  # definition of g(x) 
sign(-1.5 - in1 + in2 + 2*in3) = 1    # simplify 
-1.5 - in1 + in2 + 2*in3 >= 0     # by def: [sign(x)=1 iff x>=0] 

Normalmente si risolverebbe questa equazione per derivati ​​di calcolo, ma poiché gli ingressi in possono prendere solo i valori 0 o 1, possiamo semplicemente enumerare tutti i casi (ci sono 2^n o 8 casi):

in1 in2 in3 -1.5-in1+in2+2*in3 
----------------------------------- 
0 0 0   -1.5 
0 0 1   0.5 * 
0 1 0   -0.5 
0 1 1   1.5 * 
1 0 0   -2.5 
1 0 1   -0.5 
1 1 0   -1.5 
1 1 1   0.5 * 

Quindi otteniamo i valori di in per i quali l'espressione sopra è positiva.