Albero rosso-nero - Nero Limite di altezza

Question

Stavo leggendo wiki su Red-Black Trees.

qualcuno può approfondire il 5 restrizione:

1. Un nodo è rosso o nero.

2. La radice è nera.

3. Tutte le foglie (NIL) sono nere. (Tutte le foglie sono dello stesso colore della radice.)

4. Entrambi i bambini di ogni nodo rosso sono neri.

5. Ogni semplice percorso da un determinato nodo a una qualsiasi delle sue foglie discendenti contiene lo stesso numero di nodi neri.

Sto avendo difficoltà a capire da quando dato lo stato dell'esempio RBT dopo the final case of insertion (caso 5 su wiki) ci dà:

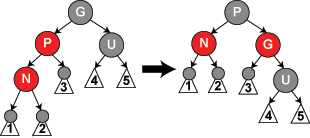
non 4 e 5 avere un nodo nero in più rispetto a 1,2 e 3?

Answer 1

1, 2, 3, 4 e 5 sono tutti sottoalberi. Sappiamo che il colore del nodo radice negli alberi 1, 2 e 3 è nero. Non sappiamo se uno qualsiasi dei nodi 1-5 sia un nodo foglia, perché questo caso di inserimento potrebbe essere stato chiamato ricorsivamente su un N che era il nonno del nodo appena inserito (da inserimento caso 3).

Prima e dopo la rotazione, le sottostrutture 1, 2 e 3 sono tutte sotto un nodo nero (G prima, P dopo) e le sottostrutture 4 e 5 sono sotto due nodi neri (G e U prima, P e U dopo). I sottotitoli 1, 2 e 3 hanno ciascuno un nodo nero in più rispetto ai sottotitoli 4 e 5.

Answer 2

L'ho letto profondamente e sembra che ci sia stato un problema con l'immagine.

Poiché N è il nodo che ha appena stato inserire significa che prima dell'ultima insert sotto P c'erano i bambini [1,3] o [2,3] (e l'inserto sia di 2 o 1 rispettivamente). Quindi in quel caso prima dell'ultimo inserto P e U devono essere stati rossi (e 4,5 sono neri).

Answer 3

Congratulazioni a James per aver decifrato il diagramma Wiki! Non è sbagliato, solo ambiguo.

La scheda "conversazione" della pagina indica che "I triangoli non sono pensati per rappresentare le foglie ma i sottoalberi Alcuni sottostrutture hanno cerchi neri in alto per indicare che la loro radice deve essere nera."

Apparentemente, i triangoli privi di cerchi rappresentano sottoalberi (incluse le foglie) per i quali il colore del nodo radice e la profondità dell'albero sono sconosciuti (e presumibilmente irrilevanti).

Quindi gli schemi semplicemente non forniscono informazioni sufficienti per dire se la "regola 5" è stata violata o meno. Dobbiamo prenderlo come un dato di fatto che non lo è.