Possiedo un ampio set di punti dati 3D a cui voglio adattarsi a un ellissoide.Inserimento di un ellissoide in punti dati 3D
La mia matematica è piuttosto scarsa, quindi ho difficoltà ad implementare il metodo dei minimi quadrati senza alcuna libreria matematica.
Qualcuno conosce o dispone di un codice che può contenere un ellissoide per i dati che posso collegare direttamente al mio progetto? In C sarebbe meglio, ma per me non dovrebbe esserci un problema di conversione da C++, Java, C#, python, ecc.
EDIT: Essere in grado di trovare il centro sarebbe di grande aiuto. Si noti che i punti non sono equidistanti, quindi prendere la media non risulterà nel centro.
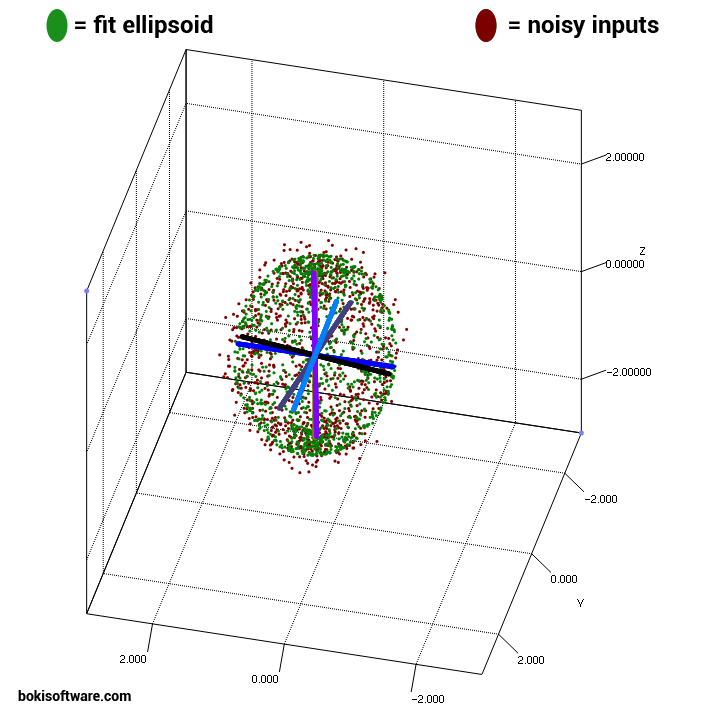
Ti aspetti i tuoi punti a cadere sulla superficie dell'ellissoide o vi aspettate i vostri punti di essere in una nube ellissoidale? – ellisbben
È possibile ruotare l'ellissoide? – Prcela
Mi aspetto che cadano sulla superficie di un ellissoide, quindi il centro è vuoto. – Hannesh